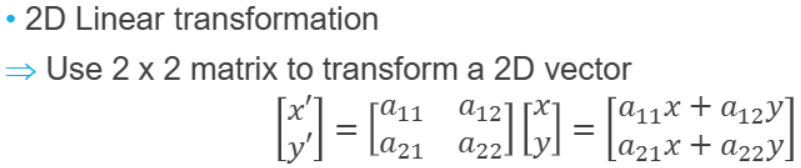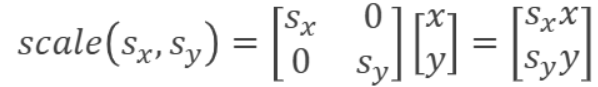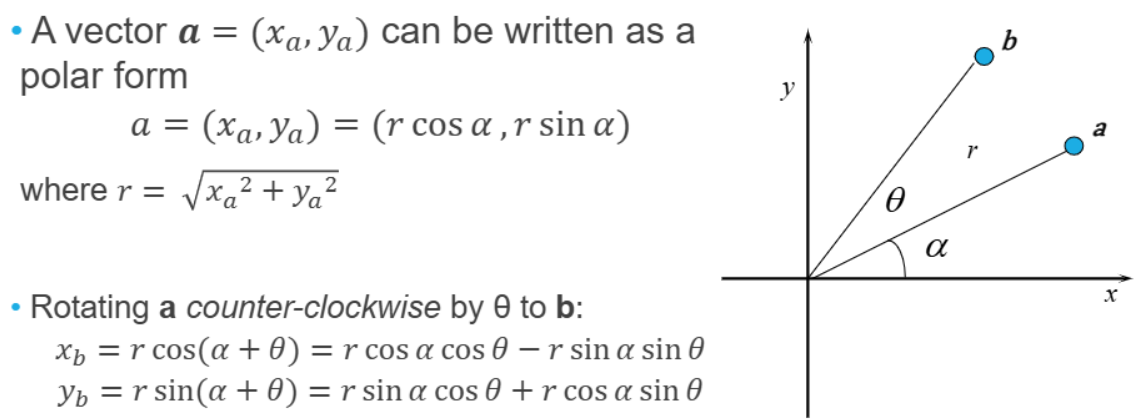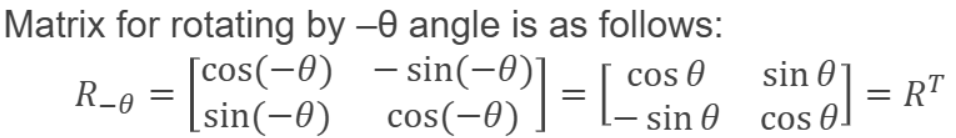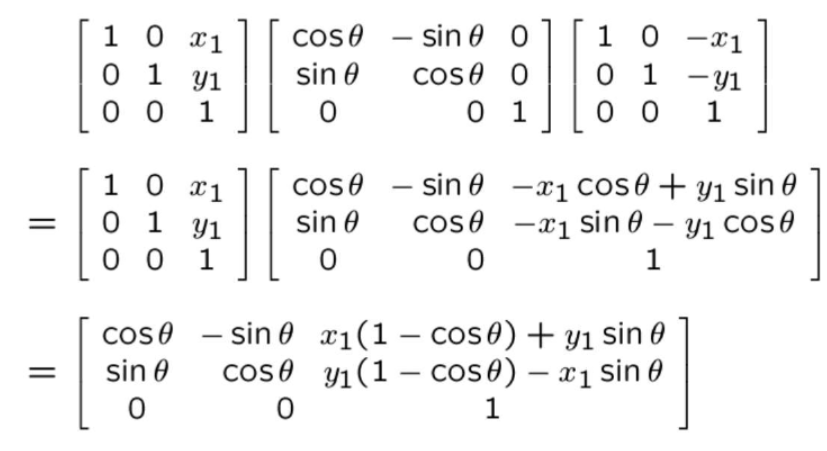[CV] Computer Vision(2-2): Image Processing - Geometric Transformation

👓Computer Vision 정리

Geometric Transformation

---

Geometric 개념 정리

---

주의: 이 슬라이드에 나와있는 점들의 좌표들은 (x-좌표,y-좌표)로 표기되어있음
즉, computer vison에서는 (y,x)로 바꿔야함

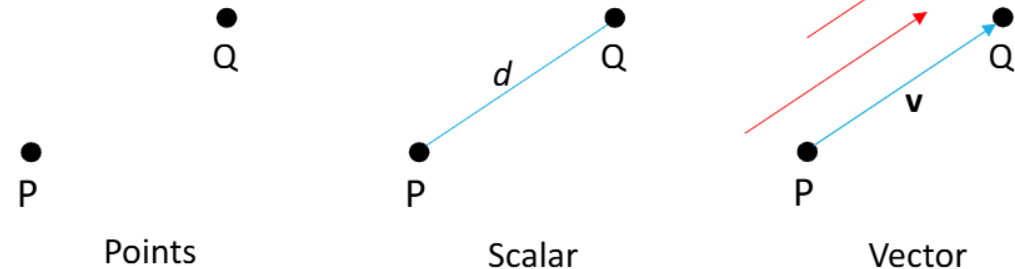
• Scalar: real number (only magnitude), (e.g., distance)
• Vector: direction + magnitude
• Point: a location in space

• 벡터의 합, 곱 등등
• 벡터 + 벡터 = 벡터 / 벡터 * 스칼라 = 벡터

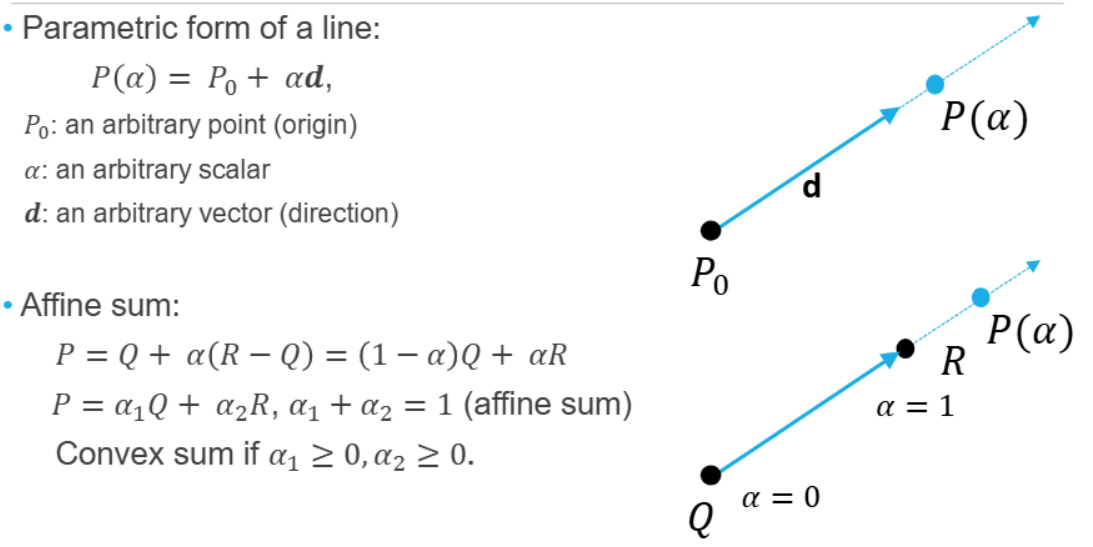
Parametric Form & Affine Sum

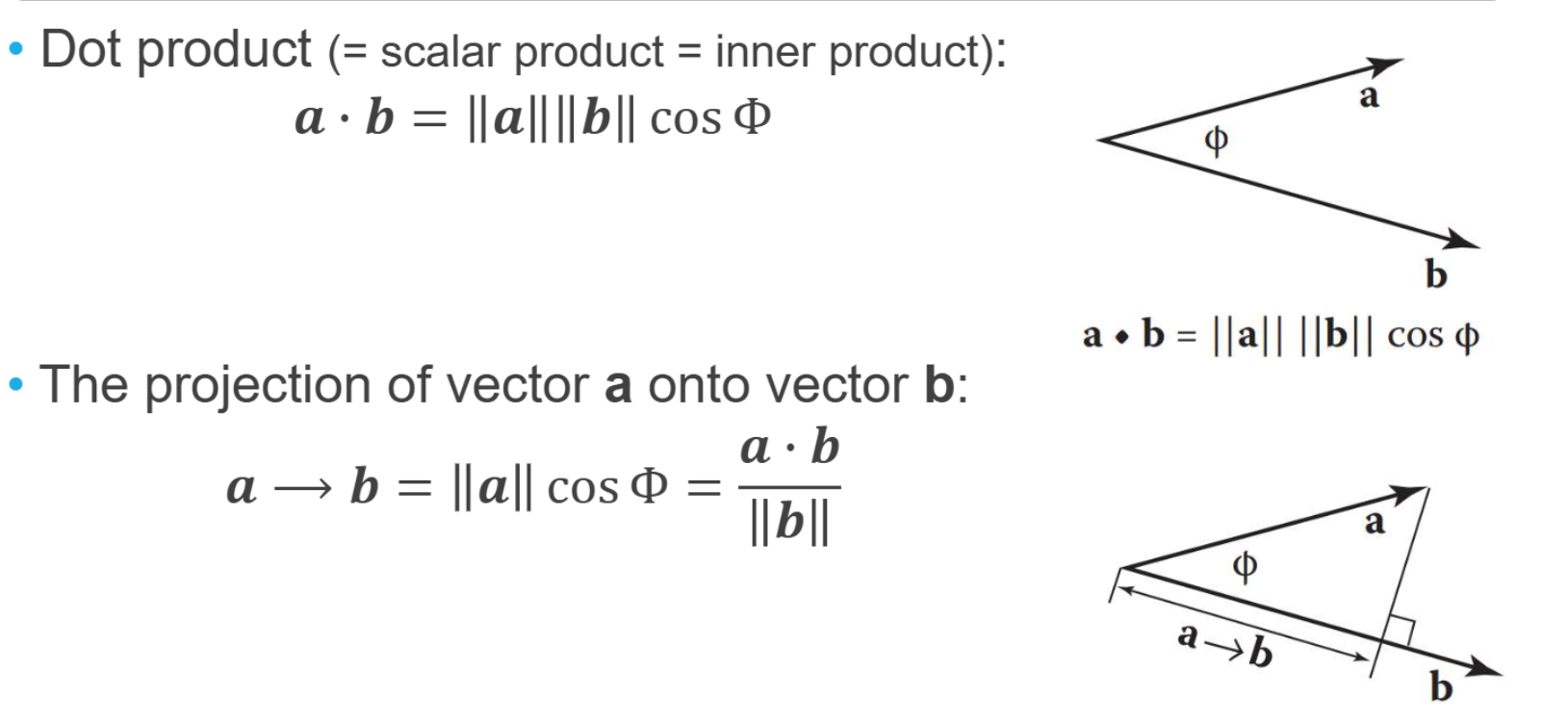
Dot Product(내적)

$\vec{a}\cdot\vec{b} = 0$ → 두 벡터 수직

Cross Product(외적)

방향: $\vec{a}, \vec{b}$에 모두 수직, 오른손 법칙 따름
결과 벡터 크기(axb): 평행사변형 넓이

2D Geometric Transformation

---

2차원 포인트는 $(x,y)$ or $x=\begin{bmatrix}x \\ y\end{bmatrix}$로 표현가능

• linear transformation: 어떤 행렬을 이용해 벡터를 변환하는 것

점에서 점으로 가는 mapping을 표현하기 위해 선형 변환을 사용
2차원의 경우 2x2을 이용해 변환
선형 변환 조건:

$L(a+b) = L(a) + L(b)$
$L(sa) = sL(a)$

2D Scaling

---

• Scaling: changes length (and direction)

대각선 방향으로 변경하고자 하는 값을 쓰면 됨

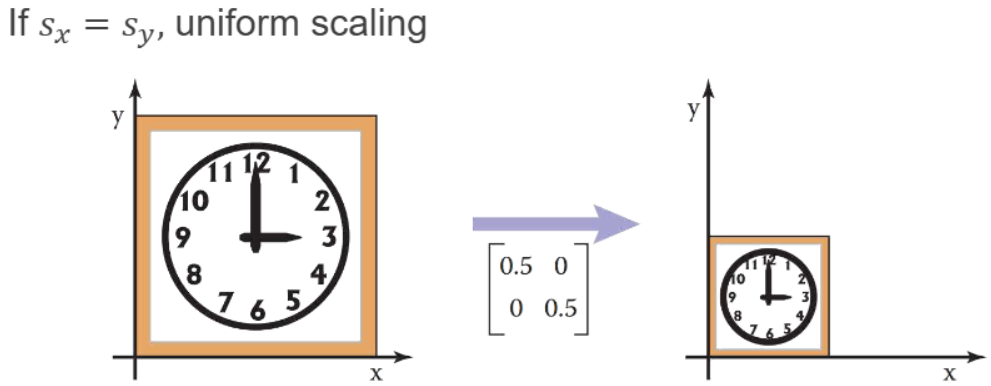
$s_x = s_y$: 균일 스케일링 (uniform scaling) → 모양은 그대로 크기만 변함
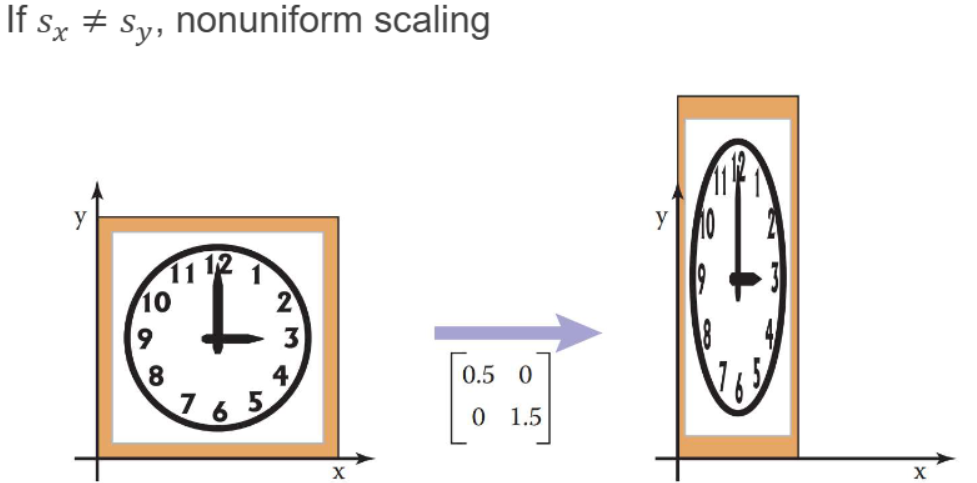
$s_x \neq s_y$: 비균일 스케일링 (non-uniform) → 형태가 찌그러질 수 있음

2D Rotation

---

• Rotation: 벡터를 각도 $\theta$만큼 반시계 방향으로 회전시키는 변환

✅ 벡터 $a=(x_a, y_a)$는 다음 두 가지 방식으로 표현 가능:

• 직교 좌표계(cartesian coordinates): $(x_a, y_a)$
• 극좌표계(polar coordinates): $(r\cos\alpha, r\sin\alpha)$
  • $r$은 벡터의 길이: $r = \sqrt{(x_a^2 + y_a^2)}$
  • $\alpha$는 x축과 벡터가 이루는 각도

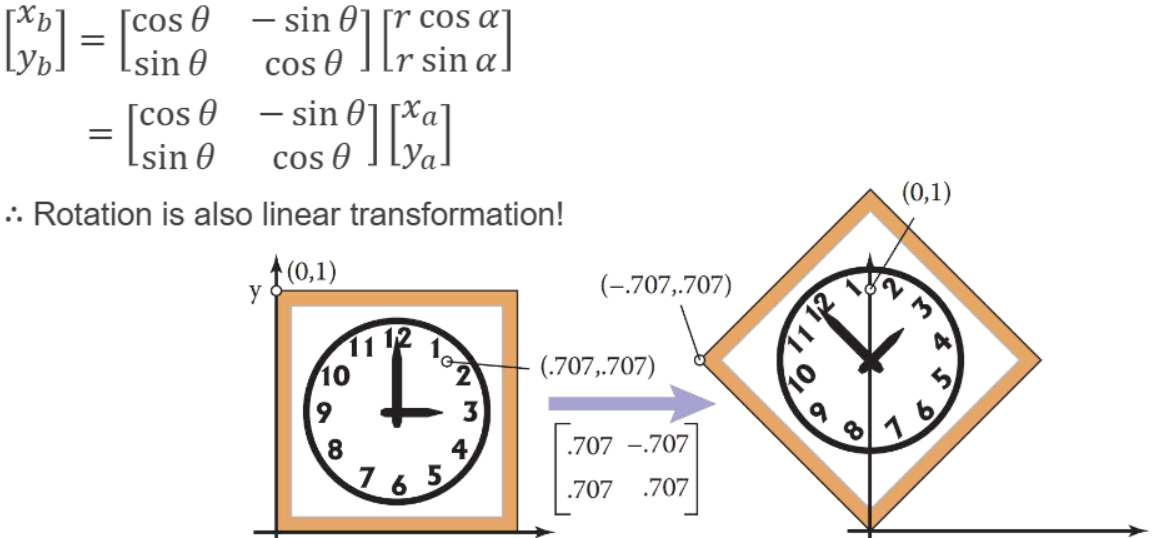
벡터 a를 각도 $\theta$만큼 반시계 방향으로 회전시킨 벡터 b는 다음과 같다:

• $x_b = r\cos(α + \theta) = r\cos α\cos\theta - r\sin α\sin\theta$
• $y_b = r\sin(α + \theta) = r\sin α\cos\theta + r\cos α\sin\theta$
• 이때 $r\cos\alpha = x_a$와 $r\sin\alpha = y_a$이므로
  • $x_b = x_a\cos\theta - y_a\sin\theta$
  • $y_b = y_a\cos\theta + x_a\sin\theta$

(xb, yb)를 matrix로 나타내면 사진과 같음 2D rotation도 2x2로 계산이 되기 때문에 linear transformation 이다.

✅ Rotation Properties

• Orthogonal matrix(직교 행렬): Two columns (rows) are orthogonal(서로 내접을 했을 때 0이 될때)
  • (cos𝜃,sin𝜃)∙−(sin𝜃,cos𝜃)=0
• inverse matrix(역행렬)
  • 

    R의 역행렬은 (-theta) 를 해주는데 그게 전치행렬과 같다. 즉, 역행렬을 구하기 위해서 그냥 전치행렬($R^T$)을 사용하면 되서 유용함

2D Shear

---

• Shear: 물체를 한 방향으로 “밀어내는” 변환, 평행사변형 모형으로 변환된다.

X, Y 방향 shear는 다음과 같다:

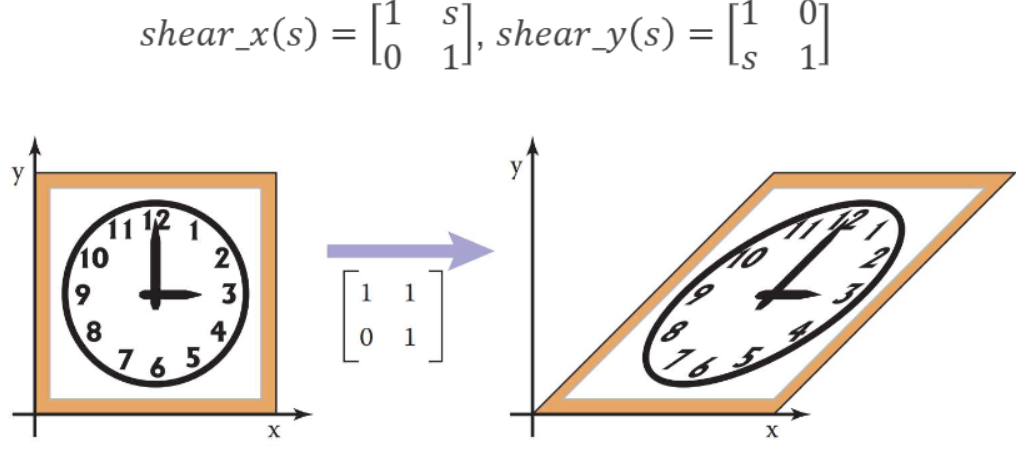
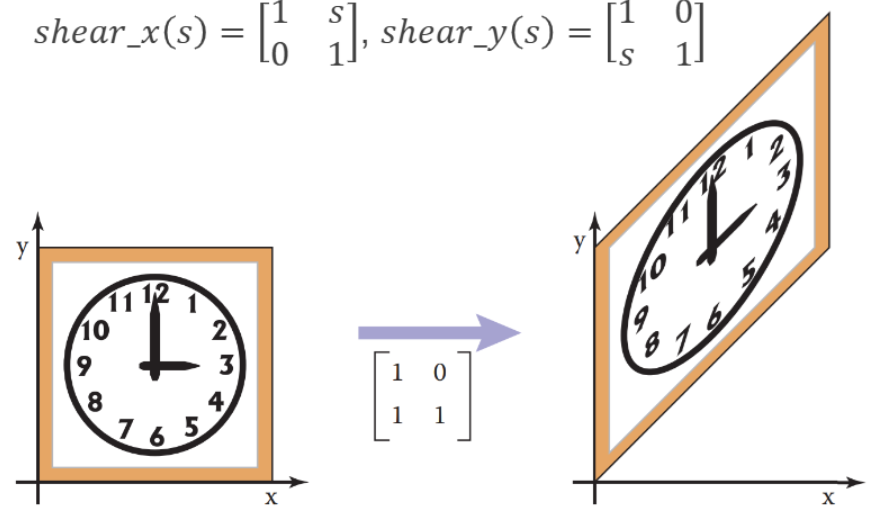
• shear_x(s) = $ \begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix}$
• shear_y(s) = $ \begin{bmatrix} 1 & 0 \\ s & 1 \end{bmatrix}$

  shear_x(s) 변환이 점 (x,y)에 적용되면 $x’ = x+sy, y’=y$ 즉 y좌표는 변하지 않고, x좌표는 y좌표에 비례하여 이동

x방향으로 shearing할때의 예시

y방향으로 shearing할때의 예시

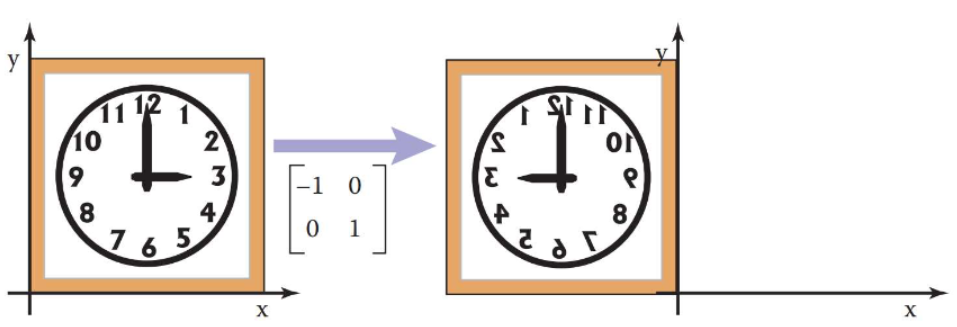
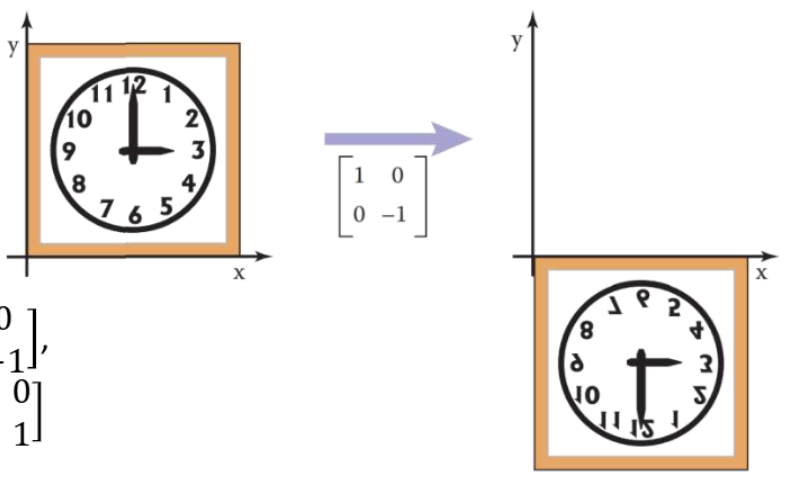
2D Reflection

---

• Reflection: 좌표 축을 기준으로 물체를 “뒤집는” 변환

X, Y 방향 Reflection는 다음과 같다:

• reflect_x = $ \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$
• reflect_y = $ \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}$

  reflect_x 변환이 점 (x,y)에 적용되면 $x’ = x, y’=-y$
  즉, y좌표만 부호가 바뀐다

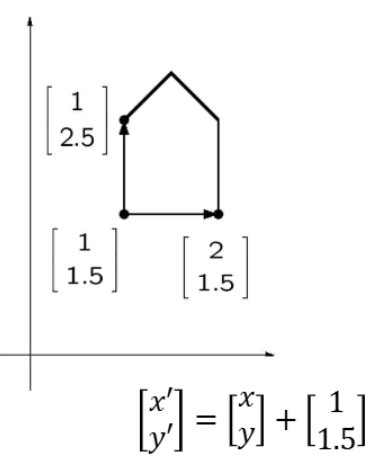
2D Translation

---

• Translation: 물체의 모든 점을 동일한 거리와 방향으로 이동시키는 변환

이동 변환 수식:

• $x’ = x + x_t$
• $y’ = y + y_t$

  $(x_t,y_t)$는 이동 벡터

일반적인 2x2행렬로는 Translation을 나타낼 수 없다!

그럼 어떻게 계산해야하나? → 그래서 나온 이론이 Homogeneous Coordinate

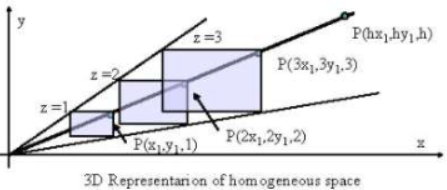
Homogeneous Coordinate

---

Homogeneous Coordinate(동차 좌표계): 동차 좌표계는 기존의 좌표계를 확정하여, 점,선,면 등을 일관된 방식으로 표현하고 변환할 수 있게 한다.

• 2차원에서 점 $x = (x,y)$는 동차 좌표계에서 다음과 같다.

$\tilde{x}$는 동차 좌표계에서의 점
$\bar{x} = (x,y,1)$은 증강 벡터(augmented vector)
$\tilde{w} \neq {0}$인 모든 $(\tilde{x},\tilde{y},\tilde{w})$는 2D 점 $\tilde{x}/\tilde{w}, \tilde{y}/\tilde{w}$를 나타낸다

즉, 동차 좌표계에서는 (2,3,1), (4,6,2), (6,9,3) 모두 2D 공간에서 같은 점 (2,3)을 나타낸다!

• 만약 $\tilde{x}$ = (x,y,0)(=$\tilde{w}$=0)이면 이 point는 ideal point 또는 point at infinity라고 불린다
  • ideal point는 방향을 나타내는데 유용하다

2D Lines

---

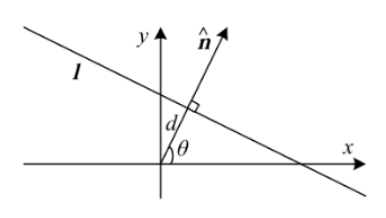
Homogeneous Corrdinate에서 2D line: $\tilde{l} = (a,b,c)$

• 직선의 방정식: $\bar{x}\cdot\tilde{l} = ax + by + c = 0$
• $\tilde{l}$을 정규화:
  • $l = (\hat{n}x, \hat{n}y, d) = (\hat{n}, d), \parallel\hat{n}\parallel = 1$

    $\hat{n}$: 직선에 수직인 단위 normal vector
    $\hat{n} = (\hat{n}x, \hat{n}y) = (\cos\theta, \sin\theta)$
    d: 원점에서 직선까지 거리
    $(\theta, d)$: 극좌표계

• $l$ = (0,0,1): 무한대에 있는 직선으로, 모든 무한대 점들을 포함함

Homogeneous Matrix

---

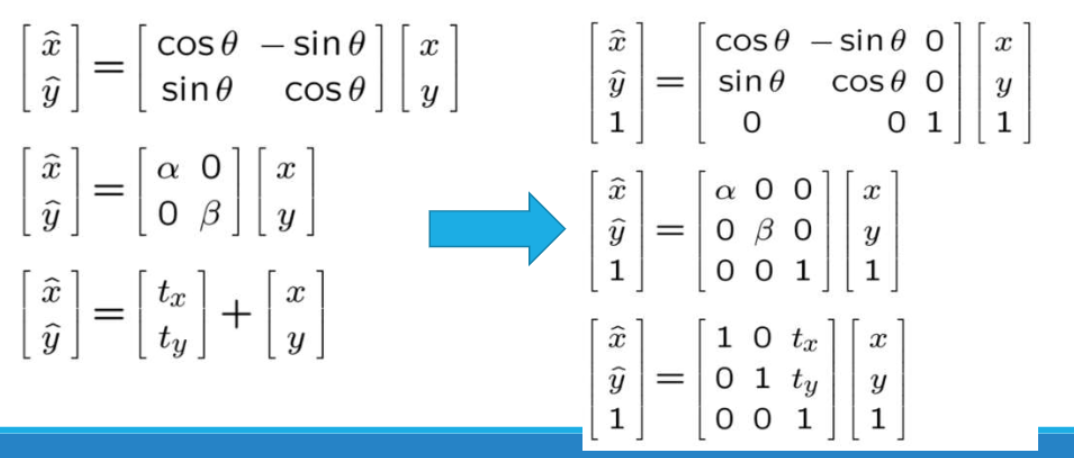
• 동차 좌표계에서의 2D 변환은 다음과 같이 변한다

순서대로 Rotation, scale, translation 변환

• 여러 변환을 조합하려면 각 변환 행렬을 곱하기만 하면 된다!

행렬을 곱할 때는 적용한 행렬의 반대 순서로 곱해야한다!

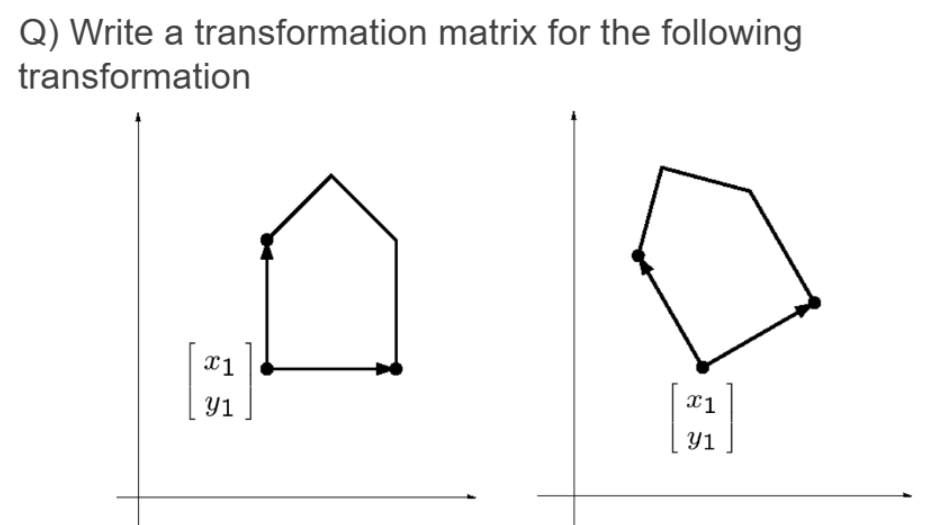
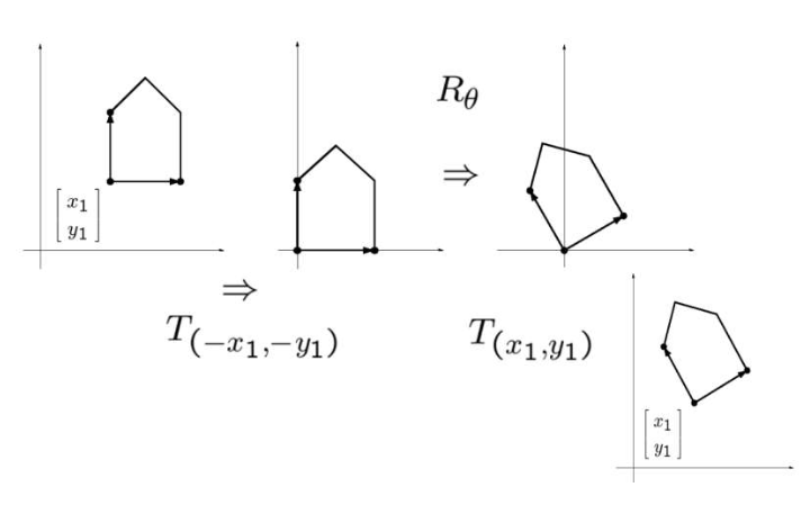
• 복합 변환 예시:

예시에서는 원점으로 이동 → Rotation 변환 → 다시 원래의 위치로 이동이므로

T_final = T_translation(원래 위치로 이동) × T_rotation x T_translation(원점 이동)

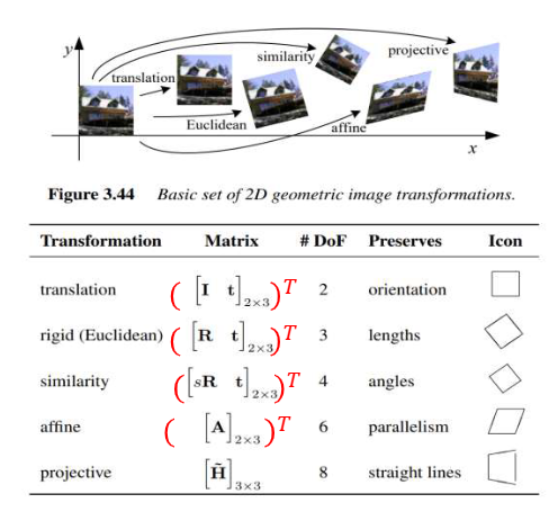
다시 CV관점으로 돌아와서 (y,x) 좌표계에서의 Homogeneous Matrix는 다음과 같다

• (y,x)좌표계에서의 복합 연산 예시:

• 2D Transformation의 종류와 특성:

  DoF는 자유도(우리가 변환하는 양)
  Similarity에서 DoF: 4(스케일 1개, 회전 1개, 이동 2개)
  전치행렬 T인 이유는 사진은 (x,y)이기 때문

그럼 이미지에 Geometric Transformation은 어떻게 적용이 되는가?

Geometric Transformation 적용

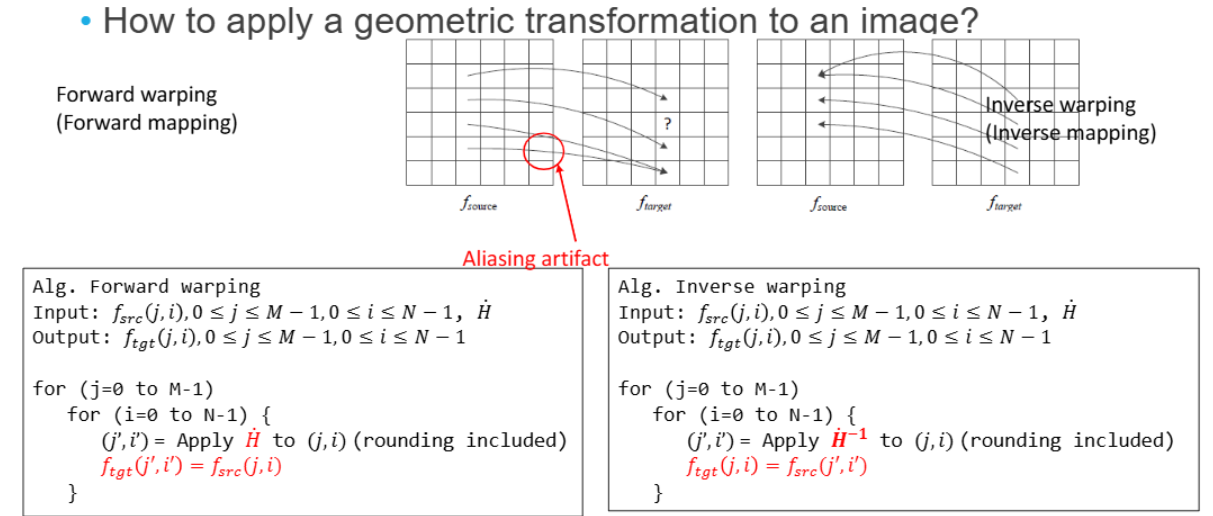
1. Foward warping:
   • 소스 이미지의 각 픽셀을 변환하여 대상 이미지의 위치로 매핑
   • 문제점:
   • 앨리어싱(aliasing) 아티팩트가 발생할 수 있다.
   • 소스 이미지의 픽셀이 정확히 대상 이미지의 픽셀 격자에 맞지 않을 수 있어 빈 공간(홀)이 생길 수 있다.
2. Inverse warping:
   • 대상 이미지의 각 픽셀 위치에 대해, 소스 이미지에서 값을 가져온다
   • 하지만 여기서도 다른 두 개의 대상 픽셀이 같은 소스 픽셀을 참조하므로 앨리어싱 발생

앨리어싱을 해결하기 위해 Interpolation으로 보완한다

Interpolation

---

Interpolation: 알려진 데이터 포인트 사이의 중간 값을 추정하는 방법

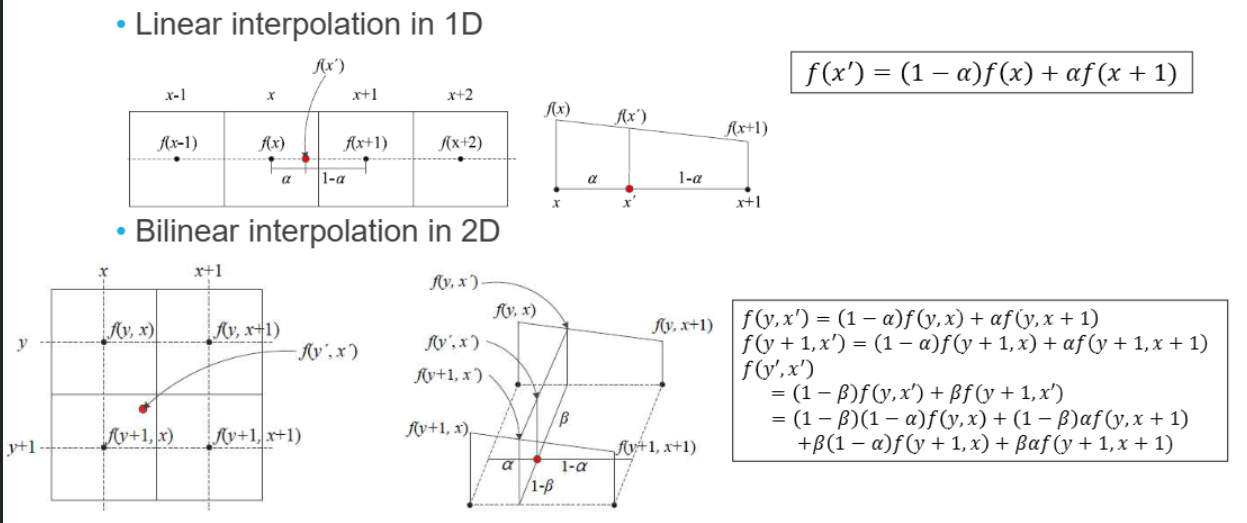
1D Linear Interpolation과 2D Bilinear Interpolation

• 1D Linear Interpolation: 두 개의 알려진 데이터 포인트 사이의 값을 직선으로 근사하여 추정

• 2D Bilinear Interpolation: 알려진 네 개의 격자점(grid points) 사이의 값을 추정

• lecture 5의 Edge Thinning은 시험 X